欧拉函数
欧拉函数的定义:1 N 中与 N 互质的数的个数被称为欧拉函数,记为φ(N)。欧拉函数公式
如果 n 的唯一分解式:
n=P1a1∗P2a2∗⋯∗Pkak
则:
φ(n)=n∗(1−p11)∗(1−p21)∗⋯∗(1−pk1)
例如φ(72),72分解质因数得:
72=23∗32
φ(72)=72∗(1−21)∗(1−31)=72∗21∗32=24
裴蜀定理
裴蜀定理,又称贝祖定理(Bézout’slemma)。是一个关于最大公约数的定理。
其内容是:
设a,b是不全为零的整数,则存在整数x,y,使得ax+by=gcd(a,b)也就是说对于方程ax+by=gcd(a,b),一定存在一组整数解。
裴蜀定理推论
a,b互质⇔gcd(a,b)=1⇔存在整数x,y,使得ax+by=1
对于方程 ax+by=z,如果满足 d∣z,那么方程一定有整数解,否则无整数解。
证明:
两边同时除以gcd(a,b),
得到:
[a/gcd(a,b)]x+[b/gcd(a,b)]y=z/gcd(a,b)
由于gcd(a,b)为a,b的最大公约数,[a/gcd(a,b)]和[b/gcd(a,b)]一定为整数,
要想x,y有整数解,所以z/gcd(a,b)也一定为整数,所以z一定是gcd(a,b)的倍数
对于方程ax+by=1,只有当整数a,b互质时,方程才有整数解。
对于方程ax+by=z,只有满足gcd(a,b)∣z,方程才有整数解.
扩展欧几里得
用于求解方程 ax +by = gcd(a, b)的解
当b=0时ax+by=a,故而一组特解是x=1,y=0
当b=0时
根据式子ax+by=gcd(a,b),同理可以得到:
bx+(amodb)y=gcd(b,amodb)
假设上面两个式子的解分别为(x,y),(x′,y′),代入得到:
ax+by=gcd(a,b),bx′+(amodb)y′=gcd(b,amodb)
因为:
gcd(a,b)=gcd(b,amodb)
所以得:
ax+by=bx′+(amodb)y′
由于
amodb=a−−∗b
因此
ax+by=bx′+(a−a∗b)y
整理一下得:
ax+by=ay′+b(x′−∗y′)
由等式相等,则各项对应相等,可以得到:
x=y′,y=x′−ba∗y′
解不定方程ax+by=c
若cmodgcd(a,b)=0,则该方程存在整数解,否则不存在整数解。
因此当cmodgcd(a,b)=0,先用扩展欧几里得算法求岀ax+by=gcd(a,b)的一组解x,y1。
则x2=x1∗gcd(a,b)c,y2=y1∗gcd(a,b)c为ax+by=c的一组解
求解过程:
ax+by=gcd(a,b)的一组解为:x1,y1
ax1+by1=gcd(a,b)
两边同除 gcd(a b),再乘以c
即得方程
a∗x1∗gcd(a,b)c+b∗y1∗gcd(a,b)c=c
因此
x2=x1∗gcd(a,b)c,y2=y1∗gcd(a,b)c
若cmodgcd(a,b)=0,则该方程存在整数解,否则不存在整数解。
因此当cmodgcd(a,b)=0,先用扩展欧几里得算法求出ax+by=gcd(a,b)的一组解x,y
则x2=x1∗gcd(a,b)c,y2=y1∗gcd(a,b)c为ax+by=c的一组解。
通解则为:
x=x2+k∗gcd(a,b)b,y=y2−k∗gcd(a,b)a
若令t=gcd(a,b)b则对于x的最小非负整数解为:
(x2modt+t)modt
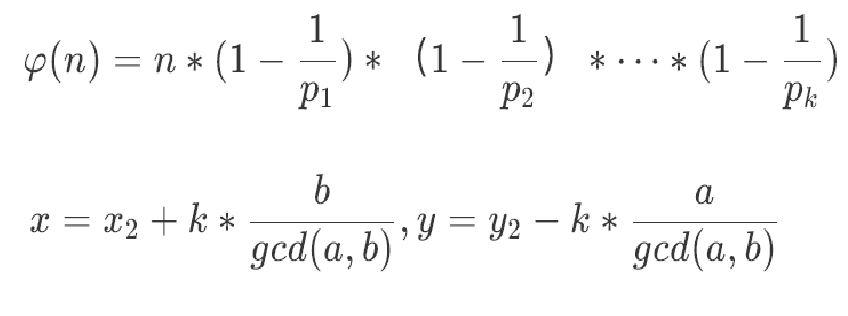





![题解:AT_abc367_c [ABC367C] Enumerate Sequences](https://cdn.luogu.com.cn/upload/image_hosting/41u3o6oe.png)